Navigation

Heimat in Rubrik:
1 2 3-Fächer: Latein 4 5 6 7 8 9

Lesetipps:
Lebendige Antike



Mitglied im




Nächste Schule Informationen über den SchulWeb-Ring
Kontakt


Dreieichschule
Gymnasium des Kreises Offenbach
Goethestr. 6, 63225 Langen
Tel: 06103-303390
Fax: 06103-3033911





In diesem Kurs, der vor einigen Jahren als WPU der Jgst. 10 stattfand, sollte unter der Leitung von Herrn Höfle u. a. die Funktionsweise eines römischen Abacus erforscht werden. Ein Nachbau erschien ihnen seinerzeit als die beste Methode.

Dazu musste man sich zuerst über die Bauweise informieren. Als Vorbild diente ein Bronze-Abacus, die Nachbildung eines römischen Originals. Genügend Material fand sich außerdem im Internet. Hilfreich war auch das Kapitel „Technisches Rechnen“ in dem Buch „Bilddokumente römischer Technik“ von Fritz Kretzschmer (Düsseldorf 1978); über römische Zahlzeichen informierte der Artikel „Zahlzeichen“ in Der Neue Pauly, Bd. 12/2, S 667ff.

Außerdem ging es darum zu erfahren, für welche Rechenarten das Rechenbrett geeignet sei und bis zu welcher Rechengeschwindigkeit man es damit bringen könne.

Zur Einführung in das Rechnen mit dem Abacus sei erklärt:
Einer, Zehner, Hunderter usw. wurden in der Antike entgegen der heute üblichen Weise bis zu viermal geschrieben, also z. B. IIII für 4, XXXX für 40 usw.
Die sog. subtraktive Schreibweise (IV für 4, IX für 9 usw.) lässt sich bei den Römern vereinzelt nachweisen, setzte sich aber erst im MA durch.
M für 1.000 findet sich ebenfalls erst seit dem Mittelalter; in der Antike verwendete man das Zahlzeichen ¥, das unserem Zeichen für unendlich ähnlich sieht.

gez.: S. Klaar
> Abacus aus Bronze, Nachbildung eines römischen Originals
> Was hat Dich motiviert, diesen WPU-Kurs zu wählen, Kamila?


Ich habe mich für den WPU-Kurs „Privatleben der Römer“ entschieden, weil mich die Lebensweise, die Kleidung und das Verhalten der Römer in der damaligen Zeit interessiert hat.


Außerdem wollte ich mit dem Selber-Bauen eines Abakus seine Funktionsweise erforschen und erfahren, wie die Römer damit umgegangen sind.

(Auf meinem Abacus ist die Zahl 6.275.381 dargestellt.)
>
Wie hast Du Deinen Abacus gebaut, Tobias?


Zuerst habe ich den Abakus auf einem dünnen Stück Holz mit einem Bleistift vorgezeichnet. Nachdem dies getan war, habe ich den Umriss des Abakus mit einer Stichsäge ausgesägt. Dort, wo die Spalten für die Perlen hinkommen, habe ich kleine Löcher gebohrt.

Durch diese Löcher konnte ich dann das Sägeblatt der Stichsäge einspannen und die Spalte aussägen. Schließlich habe ich von den beiden Seiten Löcher bis zu den Spalten gebohrt. Bevor ich dies getan habe, bemalte ich den Abakus mit schwarzer Farbe. Die Löcher waren genauso groß wie der Draht, den ich später durchgezog.

Während ich den Draht durch die Löcher geschob, fädelte ich die Perlen auf den Draht. Da die Löcher genauso groß sind wie der Draht, ist dieser auch nicht mehr herausgerutscht.
(Auf meinem Abacus ist die Zahl 7.862.992 dargestellt.)
> Bojan, wie hast du deinen Abacus konstuiert?

In der Nullstellung befinden sich die oberen Knöpfe (calculi, daher „kalkulieren“) am oberen und die unteren am unteren Rand des Abacus. Gezählt wird zum Steg hin.
Als Zahlzeichen lesen wir auf dem Steg I für 1, X für 10, C für 100, Unendlich-Zeichen od. liegende 8 (bzw. griechisches Phi) für 1.000, dasselbe Zeichen in Klammer
für 10.000, in Doppelklammer für 100.000, X links, oben, rechts umrahmt, also ein umrahmtes X für 1.000.000.



Die Spalten (columnae) sind von rechts nach links aufsteigend. Bruchrechnung mit Zwölfteln, 24steln, 48steln und 36steln ist in den beiden Spalten genz recht möglich.

In der dritten Spalte von rechts stehen die Einer (I), in der vierten die Zehner (X), in der fünften die Hunderter (C) usw. bis eine Million ¦X¦. Je ein Knopf der unteren Abacushälfte hat den Wert 1, 10, 100 usw., ein Knopf der oberen den Wert 5, 50, 500 usw.


>
Beispiel (1):
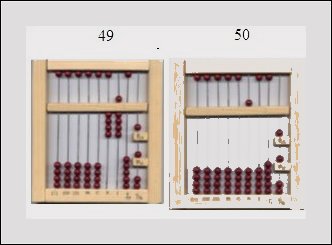
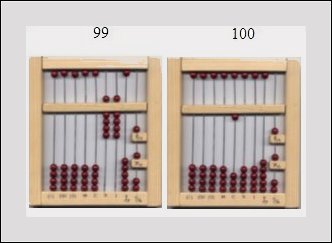
> Izzetin, wie zählt man mit dem Abacus?
Mit eins beginnend wird gezählt, indem die Einer-Knöpfe zum Steg hin nach oben verschoben werden. Bei 5 werden diese wieder nach unten geschoben, dafür wandert der Fünfer-Knopf nach unten. Wird weitergezählt werden, müssen der Reihe nach die Einer-Knöpfe bis 9 wieder nach oben wandern.

Bei 10 werden alle Knöpfe der I-Spalte in die Ausgangsposition zurückgestellt und der erste 10er-Knopf nach oben verschoben. Entsprechend verhält es sich, wenn wir von 49 nach 50, 99 nach 100 usw. zählen:
>
Beispiel (2):
>


Stefan, wie addiert man?

Beim Addieren wandten wir die beim Zählen gefundenen Regeln an. Wir schrieben die zu addierenden Zahlen in arabischen Ziffern auf. Das Prinzip läßt sich aber problemlos auf römische Zahlen übertragen. Denn wie wir erkannten, rechneten die Römer dekadisch, wenngleich sie auch nicht dezimal schrieben.

Am einfachsten erschien es uns, die Zahlen nicht der Reihe nach zu addieren, sondern so, wie wir heute schriftlich addieren: zuerst alle Einer, dann alle 10er, 100er usw. Wir fanden schnell heraus, dass es oft schneller geht, z. B. die Addition 7+8 durch 7+10-2 zu ersetzen oder 800+500 durch 800+1000-500.

Für die Additionsaufgabe 3875 + 7218 + 9676 ergeben sich folgende Einstellungen:

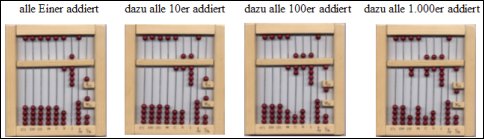Diese Abbildung zeigt das Ergebnis: 20.769. Eine Aufgabe wie die oben schafften wir in 35 Sekunden. Mit dem Taschenrechner geht es natürlich etwas schneller.


>


Colin B. erklärt, wie subtrahiert wird:

Beim Subtrahieren verfuhren wir wie ähnlich wie beim Addieren, nur fingen wir mit der höchsten Zehnerpotenz an. Auch hier war es oft praktischer oder gar notwendig, z. B. 15-7 durch 15-10+3 zu ersetzen oder 3.000-600 durch 3.000-1.000+400.

Mit etwas Erfahrung konnten wir so uns viel Hin- und Herschieben der calculi ersparen und es zu einer erstaunlichen Rechengeschwindigkeit bringen.



Für die Subtraktionsaufgabe 85.675-17.928-23.817 ergeben sich folgende Einstellungen:
Webteam, aktualisiert, 22.6.2007